A Theory of Dynamic Product Awareness and Targeted Advertising
Rapid technological advances in advertising have enabled firms to better target those consumers most likely to buy their products. We develop a novel framework of demand as a network, where heterogenous consumers dynamically become ``aware’’ of differentiated products, expanding their choice sets and improving on their possible matches thanks to advertising.
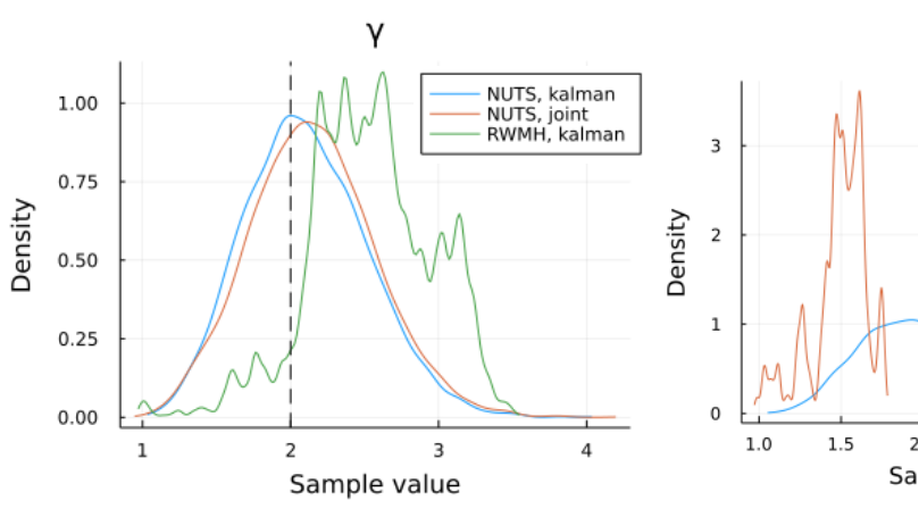
Spooky Boundaries at a Distance: Exploring Transversality and Stability with Deep Learning
In the long run, we are all dead. Nonetheless, even when investigating short-run dynamics, models require boundary conditions on long-run, forward-looking behavior. In this paper, we show how deep learning approximations can automatically fulfill these conditions.
Information, Trading Technology, and Financial Sector Profits
Common wisdom in financial markets is that there is temporary arbitrage, or at least a skewed split of surplus, that can be exploited by agents using private information. This is reflected in the enormous investment in market data and trading technologies in the financial services sector. However, Milgrom and Stokey (1982) and Grossman and Stiglitz (1980) show that asymmetric information alone cannot be exploited by an agent in a Walrasian equilibrium, and that this prevents private gains to investment in information precision - which, in turn, can make markets informationally inefficient. This research attempts to resolve this paradox by introducing a model with asymmetric information and precision, but where the micro-structure of market clearing introduces private returns to investment in signal precision, and frictions in the speed of information diffusion are reflected in the aggregate price distribution.
Complexity Constrained Walrasian Equilibria: Welfare Loss and Market Structure
Walrasian market clearing requires solving a large-scale optimization (or, potentially, fixed-point) problem. Algorithms for the auctioneer to solve these problems may be bounded by the curse-of-dimensionality - known in computer science as infeasibility - or, with some luck and structure, polynomial algorithms in number of agents and/or the number of signals. Moreover, high information content of idiosyncratic states could exhaust the limited (information-theoretic) bandwidth or computational resources of the auctioneer. The core questions in applying computational bounds to equilibrium are: (1) if there are a huge number of agents, do limitations on the computability and/or bandwidth in calculating the equilibrium lead to misallocation?; and (2) do these constraints change the optimal market structure?.
Equilibrium Imitation and Growth
The least productive agents in an economy can be vital in generating growth by spurring technology diffusion. We develop an analytically tractable model in which growth is created as a positive externality from risk taking by firms at the bottom of the productivity distribution imitating more productive firms. Heterogeneous firms choose to produce or pay a cost and search within the economy to upgrade their technology. Sustained growth comes from the feedback between the endogenously determined distribution of productivity, as evolved from past search decisions, and an optimal, forward-looking search policy. The growth rate depends on characteristics of the productivity distribution, with a thicker-tailed distribution leading to more growth.
Catch-up and fall-back through innovation and imitation
Will fast growing emerging economies sustain rapid growth rates until they “catch-up” to the technology frontier? Are there incentives for some developed countries to free-ride off of innovators and optimally “fall-back” relative to the frontier? This paper models agents growing as a result of investments in innovation and imitation. Imitation facilitates technology diffusion, with the productivity of imitation modeled by a catch-up function that increases with distance to the frontier. The resulting equilibrium is an endogenous segmentation between innovators and imitators, where imitating agents optimally choose to “catch-up” or “fall-back” to a productivity ratio below the frontier.